Deep Learning Notes 2 Linear Classificaiton
In this post, I’ll coptinue to share my notes in CS231N course that is thought at Stanford University.
Since kNN is not a good choice for image classification a more powerful method is developed. In this method there are two main components.
Score function: Maps the raw data to class scores Loss function: Quantifies the agreement between the predicted scores and the ground truth labels.
Main idea is optimize the problem by minimizing the loss function wrt parameters of the score function.
Linear classifier Linear classifier computes the score of each class for all pixel values for all 3 channels. Without the bias value, all the lines cross the origin. Whereas the W, weight values, make the lines move on the lines. Another interpretation of the weights W is a template or prototype for each classes. The score of each class is then calculated by the dot product or inner product of image with each template. So, linear classification can be called as template matching, where the templates are learned.
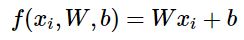
Bias Trick Since it is hard to keep track of both bias b and weights W, extending x in the above equation and adding 1 extra dimension to vector x. With our CIFAR-10 example, xi is now [3073 x 1] instead of [3072 x 1] - (with the extra dimension holding the constant 1), and W is now [10 x 3073] instead of [10 x 3072]. The extra column that W now corresponds to the bias b.
Image data preprocessing It is common to normalize the input vector by subtracting mean from every pixel. This is centering the data, can also be called as mean image.
Loss Function We want to match our calculations with ground truth labels in the training data. We will calculate the error in our predictions with loss function, aka cost funtion or objective.
Multiclass Support Vector Machine loss
References
[1] http://cs231n.github.io/linear-classify/
