Bayes Theorem and Naive Bayes Classifier
One of the hardest topics in NLP (Natural Language Processing) is the Sentiment Analysis topic. It is to decide whether the given document, sentence, aspect, or word is positive, neutral or negative in terms of sentiment. Sentiment analysis is used for spam checking in e-mails and other areas is real life. For this, Naive Bayes Classifier is used and it is based on the Bayes Theorem as the name suggests. In this post, I’ll try to explain them in detail.
Joint Probability
P(A,B) is called the joint probability distribution in probability theory. This means that, what is the probability of event A and event B to occurs at the same time. In joint probability, the probabilities of A and B are multiplied to find the joint probability.
Bayes Theorem
P(A|B) is the conditional probability. It means the probability of A given B occurred. So, when we are certain that event B happen, what is the probability that event A will occur. This is sometimes hard to compute. However, Bayes’ rule enables us to compute P(A|B) in terms of P(B|A), which we may already know. Sometimes P(a)=P(A|B), and this is when events A and A are statistically independent.
-
P(A|B) is called posterior belief, probability of event after evidence is seen
-
P(A) is called prior belief or priori, probability of event A before evidence is seen
-
P(B|A) is called likelihood that is B will occur if A is true
-
P(B) is called evidence
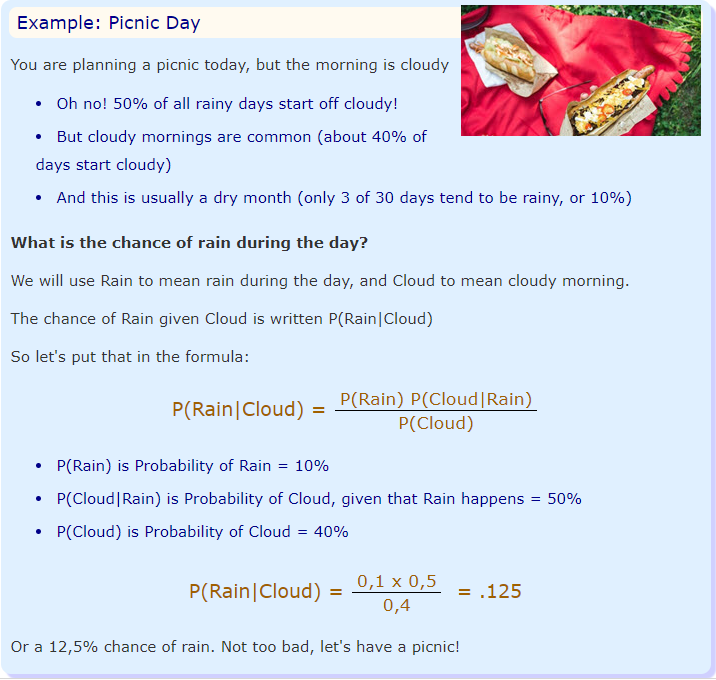
P(A|B) = ( P(A)*P(B|A) ) / P(B)
Which tells us: how often A happens given that B happens, written P(A|B) When we know: how often B happens given that A happens, written P(B|A) and how likely A is on its own, written P(A) and how likely B is on its own, written P(B)
Difference between P(A|B) and P(A,B)
Suppose we are throwing 2 6-sided dice and suppose that condition ‘A’ is the the numbers of the top faces of the two dice sum up to 7, and condition ‘B’ is that die number 2 shows 1.
What is P(A,B)? There is only 1 way in which this can happen and it is die 2 must show a 1, and the other a 6. As there are 36 possibilities that we all assume to have equal probability, P(A,B) = 1/36.
What is P(A|B)? We know that die 2 is a 1. So the only way for the sum to be 7 is for die 1 to be a 6. As there are 6 possibilities for die 1, P(A|B) = 1/6 [2]
Naive Bayes’ Theorem
The term naive is used for real because there is a naive assumption is this theorem, which usually is not correct in real world, but makes the computation very easy. Therefore, it is highly used while solving real world problems. The naive assumption is all the events are independent of each other.
Therefore Naïve Bayes Classifier makes two simplifying assumptions
- Bag of Words Assumption Assume word position doesn’t matter
- Conditional Independence (Naïve Bayes) Assumption Assume the feature probabilities 𝑃(𝑓𝑖|𝑐) are independent given the class 𝑐
References
[1] https://www.mathsisfun.com/data/bayes-theorem.html
[2] https://math.stackexchange.com/questions/43623/what-is-the-difference-between-pa-b-and-pab
[3] https://www.geeksforgeeks.org/naive-bayes-classifiers/
